Types of Symmetry
We will learn about all types of
symmetry of various shapes in geometry. The explanation will help us to
understand the different types of symmetrical shapes which possess or
does not possess linear symmetry, point symmetry and rotational
symmetry.
Name and draw the shape which possesses linear symmetry, point symmetry and rotational symmetry?
1. Line segment:
(i) Linear symmetry possesses 1 line of symmetry i.e. perpendicular bisector of PQ
(ii) Point symmetry possesses point symmetry mid-point O of line segment PQ
(iii) Rotational symmetry possesses rotational symmetry of order 2 about O.
2. Rectangle:
(i) Linear symmetry possesses 2 lines of symmetry. Line joins the mid-point of 2 parallel sides.
(ii) Point symmetry possesses point symmetry with point of intersection of diagonals as the centre of symmetry.
(iii) Rotational symmetry possesses rotational symmetry of order 2.
3. Rhombus:
(i) Linear symmetry possesses 2 lines of symmetry i.e. 2 diagonals of the rhombus
(ii) Point symmetry possesses point symmetry with point of intersection of diagonals as the center of symmetry.
(iii) Rotational symmetry possesses rotational symmetry of order 2.
4. Square:
(i) Linear symmetry possesses 4 lines of symmetry, 2 diagonals and 2 lines joining the mid-point of opposite sides.
(ii) Point symmetry possesses point symmetry with point of intersection of diagonal.
(iii) Rotational symmetry possesses rotational symmetry of order 4.
5. Circle:
(i) Linear symmetry possesses infinite lines of symmetry of order 4
(ii) Point symmetry possesses point symmetry about the center O
(iii) Rotational symmetry possesses rotational symmetry of an infinite order
2. Name and draw the shape which possesses linear symmetry but no point symmetry and rotational symmetry?
2. Name and draw the shape which possesses linear symmetry but no point symmetry and rotational symmetry?
1. An angle:
(i) Linear symmetry possesses
1 line of symmetry i.e. angle bisector
(ii) No point symmetry
(iii) No rotational symmetry
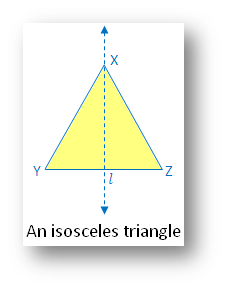
2. An isosceles
triangle:
(i) Linear symmetry possesses
1 line of symmetry i.e. perpendicular bisector l.
(ii) No point symmetry
(iii) No rotational symmetry
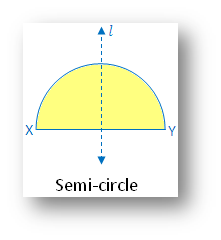
3. Semi-circle:
(i) Linear symmetry possesses
1 line of symmetry i.e. perpendicular bisector of the diameter XY
(ii) No point symmetry
(iii) No rotational symmetry
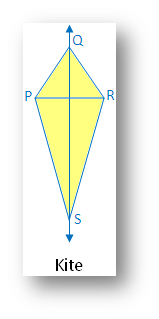
4. Kite:
(i) Linear symmetry possesses
1 line of symmetry i.e. diagonal QS
(ii) No point symmetry
(iii) No rotational symmetry
5. Isosceles
trapezium:

(i) Linear symmetry possesses 1 line of symmetry. Line XY
joins the mid-point of 2 parallel sides.
(ii) No point symmetry
(iii) No rotational symmetry
3. Name and draw the shape which
possesses linear symmetry and rotational symmetry but no point symmetry?
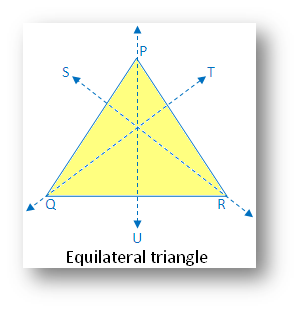
Equilateral triangle:
(i) Linear symmetry possesses 3 lines of symmetry i.e. the 3
medians of the triangle.
(ii) No point symmetry
(iii) Rotational symmetry possesses rotational symmetry of
order 3.
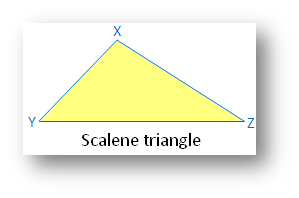
4. Name and draw the shape which
does not possess linear symmetry, point symmetry and rotational symmetry?
Scalene triangle:
(i) No linear symmetry
(ii) No point symmetry
(iii) No rotational symmetry
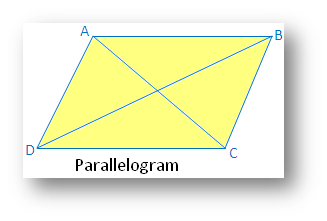
5. Name and draw the shape which
does not possess linear symmetry but possesses point symmetry and rotational
symmetry?
Parallelogram:
(i) Linear symmetry: No
linear symmetry
(ii) Point symmetry possesses point symmetry with point of
intersection o